I'm a huge fan of Savage Worlds and the more that I play it, the more I find that the system falls into the sweet spot of where I am in my gaming life right now. I need a game that is relatively intuitive, that is flexible, that has some good tactical rules, has some good "abstract" rules, and can be played in a hurry. Savage Worlds is one of those rules sets. Recently, my group has been playtesting FENG SHUI for Atlas Games and playing around with the Accursed setting for Savage Worlds. In the near future, I hope that my group will be interested in playing a Savage Worlds based supers game. Before I ask my players to make that leap, I do want them to be more comfortable with Savage Worlds as a system. Super hero campaigns push any rules set to the limit and demand a lot of players with regard to knowledge of the rules set, so I won't likely be asking the players until early next year.
When I do run the campaign, I will likely be running a Marvel game or a Marvel/DC mashup game and so I'll be converting a number of characters as well as using some conversions I find online. As I've mentioned a couple of times in the Make Mine Savage series, one of the challenges in character conversion is avoiding "power exaggeration." This occurs when a player/GM substitutes their own power fantasy about a given character to set the assumed baseline instead of starting with the game's mechanical baseline and moving from there. The prime example of a power fantasy setting a baseline in relative power discussions often occurs when chatting about whether The Hulk or the Juggernaut is stronger. For gamers/comic fans of a certain age, one only has to wait until the second or third round of discussion before the scene from Secret Wars where The Hulk holds up a mountain range comes into play.
Let's just say that if you are setting your baseline for what The Hulk needs to be capable of at "Fifty Billion Tons" as a mechanical necessity, this is beyond even the Cosmic Level of Savage Worlds which would set d12+12 at 10,000 tons. Were I adjudicating the mountain scene above, I'd use the Dramatic Tasks rules and apply appropriate penalties with each failure on The Hulk's behalf equating to a level of fatigue.
So where would we set The Hulk within a Savage Worlds framework? What is the appropriate level for The Hulk? The old Official Handbook of the Marvel Universe, as well as the old FASERIP system, place The Hulk at the 100 Tons range which is d12+9. This is useful as far as it goes, but doesn't really tell us a lot. This is especially true if the GM is using my alternate "dials" with regard to lifting or is using the following Edge:
Super-Brawny
Requirements: Novice, Strength and Vigor d12+
Your super-bruiser is significantly stronger than other characters in the setting. This is either because the character is large for his or her size category, or because she or he is very fit. The character is more resistant to damage than other characters (+2 to Toughness). Additionally, the character can lift or carry more that most characters with the same strength. This character can carry 10 times the amount listed on the Superhuman Strength chart. This edge may be taken multiple times where the multiplier stacks logarithmically (2xSuper-Brawny = x 1000 lift, but the character only receives the Toughness bonus once. If you wish, you can require the expenditure of a bennie and a STR roll at -6 to activate this ability. A failure on the roll equals 1 level of fatigue. Characters who become incapacitated from this fatigue must rest until they recover.
I'm a fan of the above Edge because it allows for increased carry/lift capacity without altering the underlying damage mechanics of the game. One of the seeming truisms of comic books is that really strong characters, characters capable of lifting battleships, often punch street level heroes without turning them into paste. This emulates that aspect of the game.
A feat like the above, gives a tool that allows Savage Worlds to accommodate what The Hulk can lift, but it does little to tell us what The Hulk's combination of Strength and Damage should be. To establish this baseline, we need to ask how easy it is for the average "Brick" to destroy some very big and very impressive vehicle or piece of hardware. I think that the M1A1 Abrams serves this purpose nicely. The Abrams weighs approximately 68 tons and for all intents and purposes serves as a nice baseline for "Super Tank." According to the Savage Worlds Rulebook, the Abrams has a Toughness of 77/58/29 (60/41/12), or in "real" terms a toughness of 17. What I mean by "real" terms, is Toughness - Armor. This is because in the Savage Worlds baseline campaign it is possible for super heroes to add the "Focus" modifier to their "Attack, Melee" combat power. The Focus modifier allows attackers to ignore armor if they make a to hit roll at a penalty. One can imagine two kinds of Supers games. In the first, all "Bricks" worth their salt have the Focus modifier. In the second, none have the modifier. For the purposes of the statistical analysis here, I will assume that they do have the Focus Modifier.
This makes our question -- assuming that the "Mean" super hero can "destroy" an Abrams with one punch -- what is the right combination of Strength and Damage to achieve this task? Destroying a vehicle requires causing 4 wounds (+16 above the Toughness) and thus requires a roll of 33. We can set our bar lower to require only that the character be able to "Damage" an Abrams, but that is a setting dial. For our current dial, let's assume 33.
Using the calculator at Anydice - set to default settings -- this provides us with the following answer:
If you prefer, you can make it d12+9 which makes x-bar 32.81 and increases the min and the max by 1 while having no effect on the standard deviation. In fact, at Attack, Melee 4d6 the amount of Strength above 12 provides a great dial for use with regard to punching holes in Abrams tanks and crippling them. If you wanted to increase the spread of pluses, you could set the baseline as:
STR d12+5 with a 5d6 Attack, Melee Power with focus.
Doing so would allow for some more control over where the supers fall in the distribution as influenced by the plus component rather than the d6 component. We can use the statistical information to decide where The Hulk falls within our super hero world. First we have to decide in what percentile we want the Hulk to fall and then we can use a procedure called "Standardizing a Normal Distribution" to give us our number. We use the following formula in this case:
Z is a value that corresponds with a certain percentage of outcomes. For example, 90% of outcomes will be equal or less than z =1.645, 95% will be less than or equal to z =1.96, and 99% will be less than z =2.57. If The Hulk is stronger than 90% of really strong people in your game, you should set z to 1.645. If stronger than 95% of crazy strong people, at 1.96 etc. We would have an equation that looks something like:
1.96 = (x - 32.99)/8.59
Hmmm....the first thing that jumps out is that this tool isn't necessarily useful for our purposes. Another way to translate this is STR = d12 + z(Bonus - 5) + 4d6 attack. What this means is that if we wanted The Hulk to be stronger than 95% of other Bricks we'd have to increase the "flat" number by 17.18 and that takes if off the chart. This tells me that the Abrams may not be the best baseline to use even if it's cool. This is largely due to the "swingy" nature of the open ended die rolls. Setting the baseline at such a high number means that we cannot use an actual distribution based on the likelihood of actual occurrence based on rolls and have it be very useful. In fact, even if we set the "average" Brick Strength at:
d12 + 2 with a 1d6 Attack, Melee
We get the following:
Even at this level we see that The Hulk would have to be (1.96*5.83) points higher than average (11ish points) to be stronger than 95% of all other Bricks.
Does this mean that we cannot use a normal distribution to help us in our converting of characters? I don't think so. I do think it means that we cannot base our conversions on a distribution of damage, rather we have to create an arbitrary distribution and mean. Let's say we keep the mean around d12 + 6 (we can set the number of d6s of Attack based on how likely we want the character to be to damage, hurt, destroy an Abrams with each of those being an added die above 2d6). Given that a "normal" can have a strength of up to d12 without Edges (we can assume that the Edges allow for characters beyond human and in the low end of Brick like Captain America), this gives us a working range of +1 to +12. If we choose 2 (arbitrarily) as our standard deviation this gives us a distribution that looks like:
If we use this in all of our calculations, we will get The Hulk as having a d12 + 6 + (1.96*2) Strength. In other words, a d12 + 10 Strength if we want him to have a Strength higher than 95% of other Supers. He'd have a d12 +9 at 90% and the percentage of people at d12 +8, +7, and +6 become larger until you hit 50% of your target population. Then the pattern repeats the other way with 95% of your Bricks having more than d12 +6 - (1.96*2) or d12 +2 Strength. That leaves only 5% of your Bricks with d12+2 or less. You can use this as a guideline to shape your campaign and should try to follow it as much as possible. This way if players as "How Strong is d12 +9?" You can answer that it is stronger than 90% of all other "Brick" caliber characters and be correct in saying so.
For me, I wouldn't set that as the baseline for my "Bricks." I'd probably set it at around 21 which is the amount of damage it takes to do 1 wound to an Abrams, but YMMV.



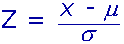
No comments:
Post a Comment