One of the chief innovations of the 3rd Edition of the Dungeons & Dragons role playing game was the incorporation of robust mechanics for combat maneuvers. Earlier editions of D&D had vague rules for parrying blows, but little to no guidance with regard to how your character could disarm an opponent or trip a foe. To be fair, some products featured what I would call "patchwork" fixes that allowed for these activities (case in point the D&D "Master's Set" for the Mentzer edition), but the mechanics didn't seem organic to the system. With 3rd edition, this changed. The maneuvers weren't always easy to accomplish for all characters, and often contained a "feat tax" to perform them without consequences, but they were clearly defined and articulated.
Paizo's Pathfinder role playing game took the basic mechanics of the combat maneuvers in 3.5 and expanded them, clarified them, and aided Gamemasters by adding listings for "Combat Maneuver Defense" and "Combat Maneuver Bonus" which helped to speed up calculations during play. They also made some small adjustments to the system.
The combat maneuvers -- other than basic strikes -- that 3.x and Pathfinder presented mechanics for include: Bull Rush, Disarm, Grapple, Overrun, Sunder, Trip, and Feint. Each of these can add some narrative dynamics to combat that empower players to control the "story" of how combat takes place and they add to the excitement of the combat experience.
A chief complaint is that 4th Edition is that the system lacks a robust system like that presented in 3.x -- in fact it is one of the complaints I hear most frequently about 4e. The typical response to those who make this complaint is that the "basic combat maneuvers" of 3.x and Pathfinder are difficult to achieve without appropriate feats and that 4e "solved this" by incorporating the effects of most of these maneuvers into the "powers/maneuvers" of the classes for which these maneuvers are appropriate. After all, the line of argument goes, making a grappling mage in 3.x/Pathfinder isn't an easy thing to do -- the feat tax "trap" and the method of calculating basic attacks -- meant that it was primarily Fighters who were good at these maneuvers.
Both the complaint and the answer are deeply flawed and don't accurately represent the problem or solution. The problem isn't that the system lacks a robust system for using these maneuvers, nor is the solution that they've incorporated the maneuvers into powers/exploits of the various classes. The problem is that 4e does have the mechanics, and they even show you how to use them on page 42 of the Dungeon Master's Guide, but that they only clearly articulate the rules for a couple of them and expect that DMs will follow the advice on page 42 for the remaining maneuvers -- or extrapolate them from the information contained in the rule books.
This is a problem of rule book drafting philosophy. As role playing games have grown as a hobby, many rules systems have become more specific in how combat maneuvers and abilities are expressed. In a manner of speaking, the mechanics of the game systems have become more like computer program subroutines and have become less subject to "DM interpretations" that may differ from group to group. The pinnacle of this style of mechanical subroutine presentation are the Hero System and GURPS, but 3.5 wasn't far behind. A key advantage to these systems is that groups can do narrative combat actions using the Rules As Written (RAW) rather than the Rules As Intended or even the Rules As Interpreted. This kind of design doesn't end rules arguments at gaming tables, but it does lessen them from the days of "rulings rather than rules." Neither the "rulings instead of rules" or "rules instead of rulings" philosophies are superior to the other, but each has its advocates and 3.x was pretty heavily on the "rules instead of rulings" side.
Surprisingly, to those who might think otherwise, 4e has a heavy "rules instead of rulings" philosophy. So much so that some gamers think of 4e as a board game or miniatures war game more than a role playing game. But the game also has a heavy -- and deep -- "rulings instead of rules" philosophy. The game tried to have the best of both worlds. It wanted the rules stability, balance, and statistical predictability of a game like Feng Shui -- where the "average" result of a character's action against a difficulty number is equal to their skill/ability score -- but they also wanted the narrative flow of a game like The Burning Wheel or Savage Worlds. In fact, once you understand the underlying math of the game it can be played entirely using the "Skill Challenge" system without ever using the combat rules -- but that is another post entirely.
The 4th Edition of D&D has a great deal of advice for playing with RAW, but they have moved beyond "Rules as Intended" or "Rules as Interpreted" and have many "Rules as Possible" which are a combination of written and interpreted rules that allow for DMs to recreate the maneuvers from the prior edition without ever creating new rules systems. To do it well, a DM does need to understand the underlying math of combat, but 4e has a pretty simple and a very static (from level to level) system. This is the game's greatest strength -- it makes designing balanced encounters easy -- and its greatest weakness.
The game provides specific examples for how Bull Rush and Grapple work in 4e, and they provide the mechanics for the rest -- but they never construct those remaining maneuvers. Page 42 of the Dungeon Master's Guide gives specific guidance on how to construct the maneuvers, but the specifics are left to the DM to construct.
The basic 4e combat math is as follows. Monsters will have an Armor Class equal to approximately 14 + level -- 15 for a Level 1 monster -- with some slight variation for the monster's "role." Monsters will have a base to hit bonus vs. Armor Class of 5 + Level -- +6 for a Level 1 monster -- and will attack other defenses at 3 + Level -- +4 for a Level 1 Monster. A Player Character will have between a 16 + Level and 20 + Level Armor Class -- depending on "role" -- and will have between a 5 + Level to 8 + bonus to hit an opponent's AC (2 less versus NADs). There is some variation of this, but these are fairly good baseline assumptions.
This means that a Monster -- attacking AC -- will be +6 vs. an AC of 17 to 21 thus hitting 30% to 50% of the time, while players will hit between 60% to 75% of the time. Tactics will modify both of these numbers upward with some roles ("Strikers") hitting 90% of the time. These percentages remain the same -- with very little variation -- throughout a character's "career." The game's progression is relatively level so that challenges have a similar character risk regardless of level, though the growth of Encounter and Daily Powers make the dynamics of combat change as the levels progress.
These assumptions are quite different than the underlying mathematical assumptions of 3.x/Pathfinder. 3.x combats are a little harder to balance, as the combat atop the Belltower in Paizo's first Adventure Path can attest, but they can be quite exciting. While high level threats in 4e might be as challenging to characters as threats were at low levels, they are still relatively narrow in tactical options -- each monster is only expected to live a certain number of rounds so there are only so many attack options given to each opponent -- whereas 3.x/Pathfinder opponents can become quite complex in their tactical offerings in later levels. Anyone who has stated up high level NPC or Dragons knows how detailed these characters can be. This level of granularity is refreshing to many players, and as an old Hero grognard I have a deep appreciation of it. This difference of granularity could be a post in and of itself, just let it be said that 4e characters are always at the same risk of death as they were at low levels and that 3.x characters encounter more tactically diverse (within a single opponent) challenges.
What is key here is that 3.x/Pathfinder is slightly harder to balance for as its combat system is looser. I'm going to use 3.x as a reference for constructing 4e versions of
So how do we bring Bull Rush, Disarm, Grapple, Overrun, Sunder, Trip, and Feint to the 4e table without actually creating new rules? How do we use the existing rules set to bring in more tactical options? Will it break the balance of the game?
I'll answer the last question first. Adding these maneuvers as powers will not break the game. There are already a number of classes, the two Essentials Rangers for example, who have "trip" effects as part of damaging powers, and the Essentials Knight has a Bull Rush capability added to one of its powers. Additionally, 4e does allow anyone to use Bull Rush and Grapple as maneuvers. We'll be using those mechanics to establish our guidelines. This leaves only Disarm, Overrun, Sunder, Trip, and Feint for us to create maneuvers for.
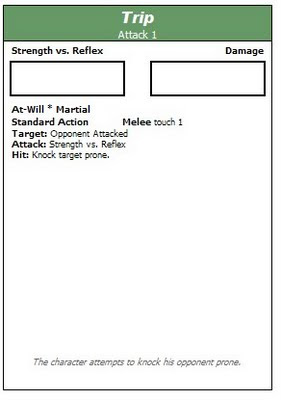
First, let's take Trip. Given that there are currently classes that -- at 1st level -- can Trip as a part of a normal attack action, it isn't game breaking to create a Trip Maneuver. Additionally, being knocked prone in 4e -- while bad -- isn't as horrible as being knocked prone in 3.x/Pathfinder.
TRIP
Essentially, Trip is an attack based on your combatant's Strength against your opponent's Reflex defense. If you hit, then you knock the opponent prone. No damage, just a prone opponent.
You might add a "Trip Training" feat that allows characters to use other statistics as the basis for tripping, just as the game has Combat Training to allow Basic Attacks to be based on alternate stats. I recommend doing so, and making it an Heroic feat.
I also recommend creating a "Sweeping Trip" power that can only be used by those who have the feat -- which I recommend be a Paragon level feat. This feat will allow a combatant to Trip anyone in a Blast 1.
It might also be wise to create feats that allow characters to used certain weapons with Trip attacks, thus gaining the proficiency bonus for those attacks. Weapons like Pole Arms and Staffs should have a "Trip Weapon Proficiency" feat, that lets you use their "Trip Weapon" feature.
Disarm is a little trickier, but not much. Given that damage for monsters is based on level, and not on weapon, a disarm attack's effect isn't just the removal of the weapon it also has an impact on damage dealt.
TRIPI would represent this through the Weakened condition, which halves the damage done by character, that can be ended by spending a move action to pick up a weapon. In essence, the monster must choose between spending an action to pick up a weapon -- or doing less damage. I would also make the attack a little more difficult than a normal melee attack and give a -2 penalty to attack rolls. Given 4e's tendency to have Non-AC Defenses 2 lower than AC, and most weapons provide a Proficiency bonus of +2, this works nicely.
Feint could easily be represented as a Weapon Attack using Strength - 2 vs. Reflex attack that grants the next attack Combat Advantage. Given that there are feats that grant Combat Advantage in easy situations, and that Doppelgangers have a Minor Action that does just this effect, it seems in line with the game's intent.
Sunder would be a Strength vs. Reflex -2 attack that specifically targeted the opponent's weapon or shield. I will give this its own post, as calculating the HP and DC of the attack requires me to look through the Essential DM's book.
Overrun is also easy, but I'd like to give it its own post as well.





2 comments:
As much as I find it's manifestation disappointing, there is a power in 4e that disarms, called Exorcism of Steel. It's a lvl 17 Fighter Encounter Exploit power, found on page 83 of the PHB.
As for tripping, here's a pretty nice build for knocking creatures prone. However, as with the disarming, it's still a pretty high level before it really comes into its own.
Beat Down (4e Optimized Character Build)
While it's nothing like it was in 3.5, it's something, I suppose.
I was reading this article, after doing a search for 4E trip mechanics, and I was wondering if you were going to revisit this with the follow up article for Sunder mechanics? Or, if you have followed it up, can you post a link to it please?
Post a Comment